# 4-49. 二叉搜索树与双向链表
> 一个有意思的点
# 题目
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。
要求不能创建任何新的结点,只能调整树中结点指针的指向。
**注意**:
- 需要返回双向链表最左侧的节点。
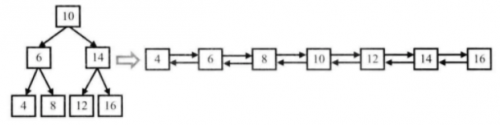
例如,输入下图中左边的二叉搜索树,则输出右边的排序双向链表。
## 思路
利用性质:**二叉搜索树的中序遍历**为`递增序列`
1. 排序链表:节点从小到大,应当使用中序遍历,访问树节点
2. 双向链表:构建相邻节点的引用关系时,设前驱节点 `pre` 和当前节点 `cur`
应当构建 `pre.right = cur`; `cur.left = pre`
3. 循环链表:链表头节点 head 和尾节点 tail,应构建 `head.left = tail` 和 `tail.right = head`
```cpp
// 打印中序遍历
void dfs(Node* root) {
if(root == nullptr) return;
dfs(root->left); // 左
cout << root->val << endl; // 根
dfs(root->right); // 右
}
```
```cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution
{
public:
TreeNode *head;
TreeNode *pre;
TreeNode *convert(TreeNode *root)
{
dfs(root);
// 如果要构造环
//head ->left = pre;
//pre ->right = head;
return head;
}
void dfs(TreeNode *root)
{
if (!root)
return;
// 根据中序遍历,此时到最左叶节点
dfs(root->left);
// 如果 pre 没有指向任何节点,则说明是在最左叶结点,开始构建链表
// 如果有指向节点,则说明是在构建的过程中
// 要设为空,若不能显示初始化为 nullptr,可以直接声明指针不初始化
if (pre) pre->right = root;
else head = root;
root->left = pre;
pre = root;
dfs(root->right);
}
};
```
# 重点
可以细看下,关于 dfs 循环处理一段

粗看三者的意义相同,但其实只有中间一段是正确的写法。
## 原因
1. 第一段,将 pre->right = root; 归入 else() 语句,则会导致在 head 安化为 root 之后,pre 得不到初始化,始终为空指针,因此再出现语句 pre->right = root 时,将会报错。
2. 第三段,也是相同的原因。
## 总结
> 思路是在找到最左叶节点时,需要同时将 pre 与 head 节点置于此节点上,再进行递归,但是如何采用 1,3 的写法,当 head 初始化后,pre 并没有得到有效初始化,因此会出现问题。
当然比较质朴的一种写法也是可以的,同时思路更加明晰。
```cpp
if (!pre)
{
head = root;
pre = root;
}
else
{
pre->right = root;
root->left = pre;
pre = root;
}
```